La percentuale di errore confronta una stima con un valore corretto ed esprime la differenza tra i due valori in percentuale. Questa misura statistica consente agli analisti di considerare l'entità dell'errore rispetto al valore reale. Viene anche indicata come errore %. Rappresenta un errore di misura.
In questo contesto, i valori stimati e corretti possono essere definiti come segue:
- Stima: misurazione, approssimazione, valore derivato sperimentalmente, ipotesi.
- Valore corretto: grandezza che è stata dimostrata o generalmente accettata come valida. Può trattarsi di una misura standard per un elemento utilizzato nei sistemi di prova o di un valore noto basato su fondamenta teoriche, come la circonferenza di un cerchio.
La percentuale di errore è una misura statistica preziosa quando la tua stima cerca di avvicinarsi a un valore noto e corretto. Infatti, quantifica quanto vicina sia una stima al valore reale. Più piccola è la percentuale, più la stima è vicina al valore reale. Al contrario, più grande è la percentuale, più la stima è lontana dal valore reale.
Per questi errori di stima possono essere responsabili diversi fattori, come lo strumento di misura, il metodo di stima, un errore umano o una combinazione di tali fattori. Se l'errore è troppo grande, può rendere le tue stime non valide e poco significative. A quel punto, devi intraprendere azioni correttive. Non esiste una soglia standard, poiché varia a seconda del campo.
Lo scopo del calcolo della percentuale di errore dipende dal contesto. Negli studi scientifici e nei progetti di gestione della qualità, gli analisti lo utilizzano per confrontare i valori misurati con quelli noti e valutare così la validità delle loro misurazioni. Anche i ricercatori possono usarlo per confrontare il valore di un esperimento con il valore teorico o vero, per dimostrare la validità dei loro calcoli sperimentali.
Per calcolare le percentuali di errore, è necessario conoscere il valore corretto. Se non lo si conosce, devi applicare un altro metodo, come la valutazione della variabilità delle misurazioni.
Ti spiegherò prima la formula in dettaglio, prima di illustrarti diversi esempi di utilizzo in vari contesti.
Il calcolo della percentuale di errore avviene in tre passaggi:
1. Calcola l'errore eseguendo Stima - Valore Corretto.
2. Dividi per il valore corretto.
3. Moltiplica il risultato per 100 per ottenere una percentuale.
A seconda del campo di studio, alcuni analisti indicano se la percentuale di errore è positiva o negativa per mostrare se la stima è maggiore o minore del valore corretto. Altri utilizzano il valore assoluto dell'errore, ossia un valore sempre positivo. Nelle equazioni seguenti per la percentuale di errore, le barre (|) indicano l'uso del valore assoluto.
Se non usi il valore assoluto dell'errore, otterrai percentuali positive quando la stima è maggiore del valore corretto, e percentuali negative quando la stima è minore del valore corretto. La forma con il valore assoluto è sempre positiva. Sappi quale tipo di valore richiede tuo campo di analisi!
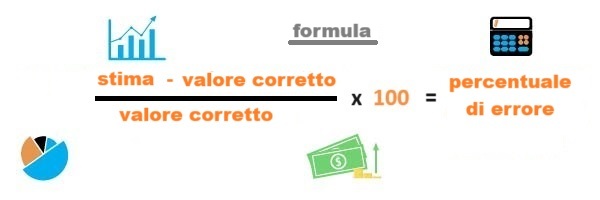
Ecco la formula per la percentuale di errore:
Percentuale di errore = ((Stima - Valore Corretto) / Valore Corretto) * 100
Per questi esempi di percentuali di errore, utilizzerò la formula che indica se il risultato è positivo o negativo, poiché fornisce più informazioni. Per ottenere il valore assoluto, rimuovi i segni negativi.
Congetture/Stime approssimative
Immagina di organizzare una festa e di stimare che parteciperanno 15 persone. In realtà, sono presenti 18 persone.
La tua stima era sbagliata del -16,67%, il che significa che era troppo bassa rispetto alla realtà.
Valutazione delle misure
Le misurazioni sono sempre imprecise, poiché sono approssimazioni del valore reale. Errori umani e i limiti degli strumenti possono contribuire a questi errori di misurazione.
Ad esempio, gli analisti nel controllo qualità valutano i loro sistemi di misurazione per il processo di ispezione, con cui vogliono assicurarsi, attraverso misurazioni valide, che i loro componenti abbiano le lunghezze corrette. Il pezzo standard che usano per i test deve avere una lunghezza di 5,0 mm. Un ispettore misura questo pezzo standard e osserva che è lungo 5,2 mm.
La misurazione dell'ispettore è distorta del 4%, poiché è troppo grande.
Se usi la percentuale di errore per confrontare le misurazioni con un elemento standard noto, piccole percentuali indicano misurazioni vicine al valore corretto. Se le tue misurazioni presentano un errore maggiore, potresti dover adattare e calibrare il tuo sistema di misurazione.
Confronto di valori sperimentali con valori noti
Nel terzo secolo a.C., Eratostene, uno scienziato greco che si trovava in Egitto, usò la posizione del sole, che aveva misurato in due luoghi diversi allo stesso tempo, per stimare la circonferenza della Terra a 43.075 km. Oggi sappiamo che la circonferenza della Terra è esattamente di 40.096 km.
La misurazione di Eratostene era sbagliata del 7,4%. È una percentuale piuttosto alta, ma per un calcolo effettuato nell'antico Egitto, è più che dignitoso!